Prior Distributions
Learning Objectives
- Learn different ways of selecting and constructing priors
1. Choosing the prior distribution
Incorporating prior information in statistical analysis is a unique feature for Bayesian modelling
- often criticized by non-Bayesians and considered as a subjective modelling choice
- in practice one should use sensitivity analysis to assess how much the posterior inference will change with varying priors
- “strategically” choosing priors that can be beneficial
- allows us to explicitly incorporate past evidence and expert knowledge
- when we are working with small samples
- we can also use sparsity promoting prior (i.e., shrinkage prior) to reduce the number of parameters to be estimated to improve estimation efficiency and avoid over-fitting
1.1 Types of priors
Generally speaking, there are two types of priors: subjective priors and objective priors.
- Subjective priors
- based on historical data
- Characterization of personal/expert opinion
- Selection of “standard” (clinical) prior distributions
- objective priors
- priors that don’t bring subjective information into the analysis
- reference priors, vague priors (e.g., flat priors, Jeffreys’ priors)
- weakly informative priors
1.2 Prior Elicitation
- Expert knowledge is a valuable source of information
- Prior elicitation is a key tool for summarizing and translating expert knowledge into a quantitative probability distribution
- Expert elicited priors can be used in the design and analysis the study.
when should we use prior elicitation?
From (Lesaffre, Baio, and Boulanger 2020)
- Factors favouring elicitation
- (no information) Inadequate empirical data are available to inform a decision (no information)
- (conflicting information) Multiple sources of empirical data are available of differing levels of relevance
- (no consensus) Lack of scientific consensus, or when reliable evidence or legitimate models are in conflict, with a need to quantify the uncertainty due to disagreement
- (when you can!) Appropriate experts (and financial resources) are available and elicitation can be completed within the required time frame
- Factors not favouring elicitation
- (not useful) A large body of empirical data (of suitable quality and relevance) exists with a high degree of consensus
- (not important) The information that an expert elicitation could provide is not critical to the assessment or decision
- (too much effort) Available expertise and/or financial resources are insufficient to conduct a robust and defensible elicitation
Methods for prior elicitation
- Fixed and variable interval methods
- expert is asked to consider a fixed value or a plausible range for the parameter
- e.g., “what is the probability that a healthy 30 year-old non-healthcare worker in Ontario will have received a COVID-19 vaccine by September 1 2021?”
- e.g., “Based on your expertise and experience, please choose the LOWER and UPPER plausible values for the number of patients who would end up being admitted to hospital out of 100 similar patients with the presented case of bronchiolitis”
- Roulette or Chips in Bins
- expert is given a “chip” and asked to place it to a distribution
- proportion of chips allocated to a particular bin priors the expert’s knowledge on the true value of the parameter (that it lies in that bin)
- generally accepted as an intuitive elicitation methods for experts
Aggregating expert judgement
There are two general approaches to summarizing the estimates from the experts.
- Aggregate the distributions
- combine these multiple distribution using mathematical aggregation, also called “pooling”
- Elicit a distribution from each expert separately and “all opinions are considered”
- easier elicitation process and minimal interaction between experts
- when individual priors are very diverse, mathematical pooling may create an average set of judgments that lacks any substantive meaning
- Aggregate the experts
- gather expert belief and elicit a single distribution, also called behavioural aggregation.
- can help to provide insights and resolve differences of opinion
- minority or extreme opinions may be lost in building a common group view
- requires a trained facilitator to manage the elicitation process and the interactions between the experts to ensure that the process is not dominated by only one or two experts
Three protocols
- Most popular. Sheffield Elicitation Framework (SHELF). The SHELF protocol is a behavioral aggregation method that uses two rounds of judgments. (O’Hagan et al. 2006)
- In the first round, individuals make private judgement
- In the second round, those judgments are reviewed before the group agrees on consensus judgement.
- Delphi Method. The Delphi is similar to SHELF as it is a behavioral aggregation method with two or more rounds except that anonymity is maintained in terms of who gave which answers.
- unlike SHELF, experts provide their judgments individually with no interaction and a pooling rule is required across expert final distributions.
Evaluating prior elicitation
Reference: Methods to elicit beliefs for Bayesian priors: a systematic review (2010), by johnson et al. (Johnson, Tomlinson, Hawker, Granton, and Feldman 2010).
- Reviewed prior elicitation on validity, reliability, responsiveness, and feasibility
Example expert elicitation from (Johnson, Tomlinson, Hawker, Granton, Grosbein, et al. 2010)
1. Participants
- single centre 12 academic specialists at the University of Toronto who treat systemic sclerosis (scleroderma)-associated pulmonary arterial hypertension (SSc-PAH) and idiopathic pulmonary arterial hypertension (IPAH) patients were recruited (single centre)
2. Procedure
A face-to-face interview was conducted with each participant using a standardized script
Conducted a sample questionnaire (pre-run) on unrelated clinical example to introduce the questions and process to participants.
Design and deliver questionnaires for elicitation (focus on clarity)
- “Question 1. For an average group of newly diagnosed scleroderma patients with pulmonary arterial hypertension treated with the standard of care at your institution but not treated with warfarin, what do you believe is the probability of being alive at 3 years? Please indicate your answer by putting an X on the line.”
- “Question 3. There may be some uncertainty around your estimate of survival. You may believe that the probability of survival could be a little lower or a little higher. Please indicate the lower boundary of your estimate for which you believe there is very little probability that the true estimate could be less than. Please indicate the higher boundary of your estimate for which you believe there is very little probability that the true estimate could be greater than. You have indicated that the lower boundary is X% and the upper boundary is Y%.”
Assess measurement properties
- face Validity
- e.g., do you feel that this questionnaire evaluated your belief about the effect of warfarin on survival in idiopathic and/or SSc-PAH?
- convergent construct validity
- What overall effect do you believe warfarin has on 3-year survival? Improves survival, worsens survival or has no effect on survival. Comparing results from this question to the elicitated belief and see if they match!
- expected moderate to good agreement between the two questions categorizing the effect of warfarin on survival
- feasibility
- e.g., how long it takes to complete the questionnaire
- reliability
- Test reliability of the elicitation procedure was tested by administering the questionnaire to participants on two occasions 1-2 weeks apart.
- face Validity
3. Results
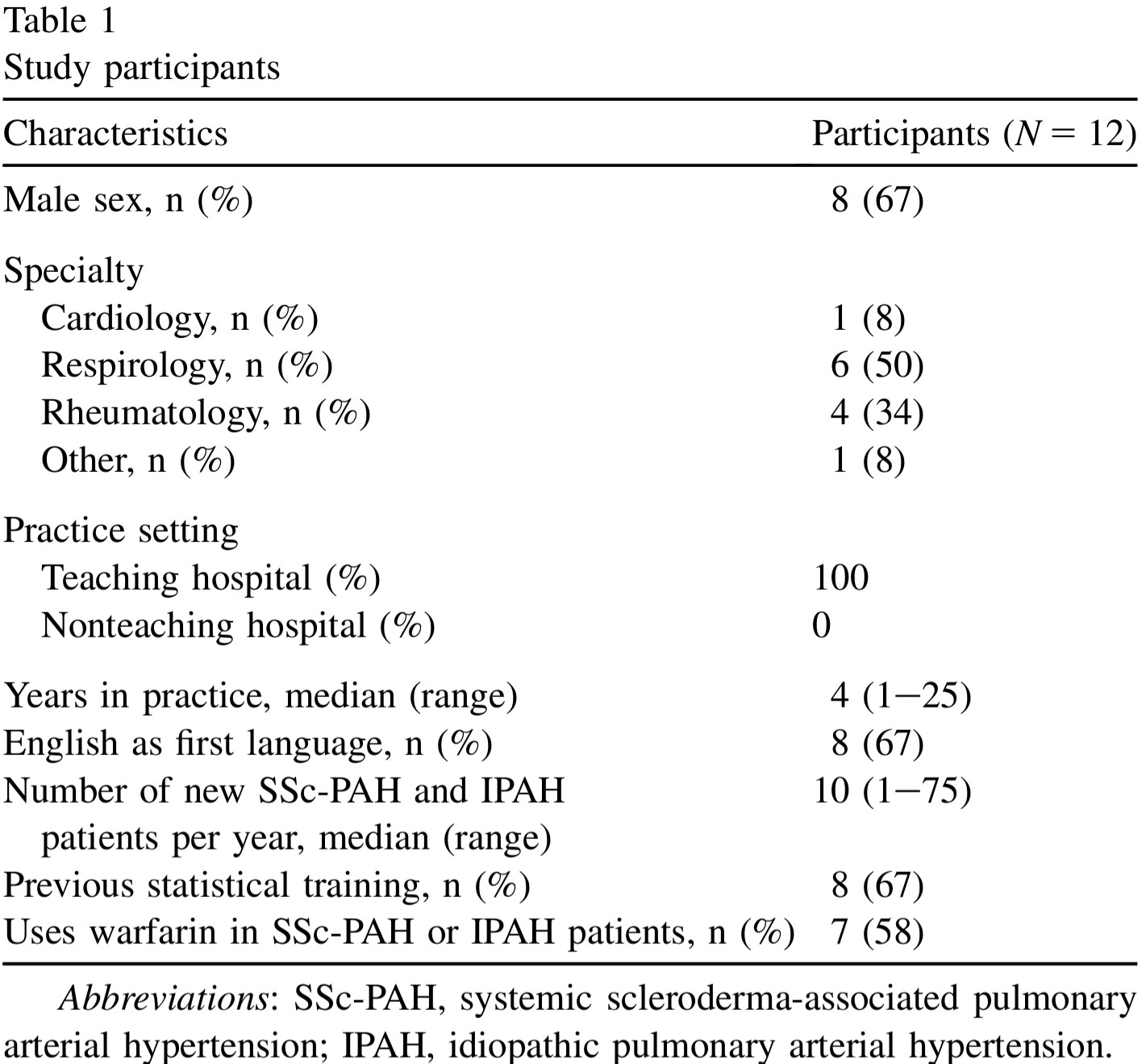
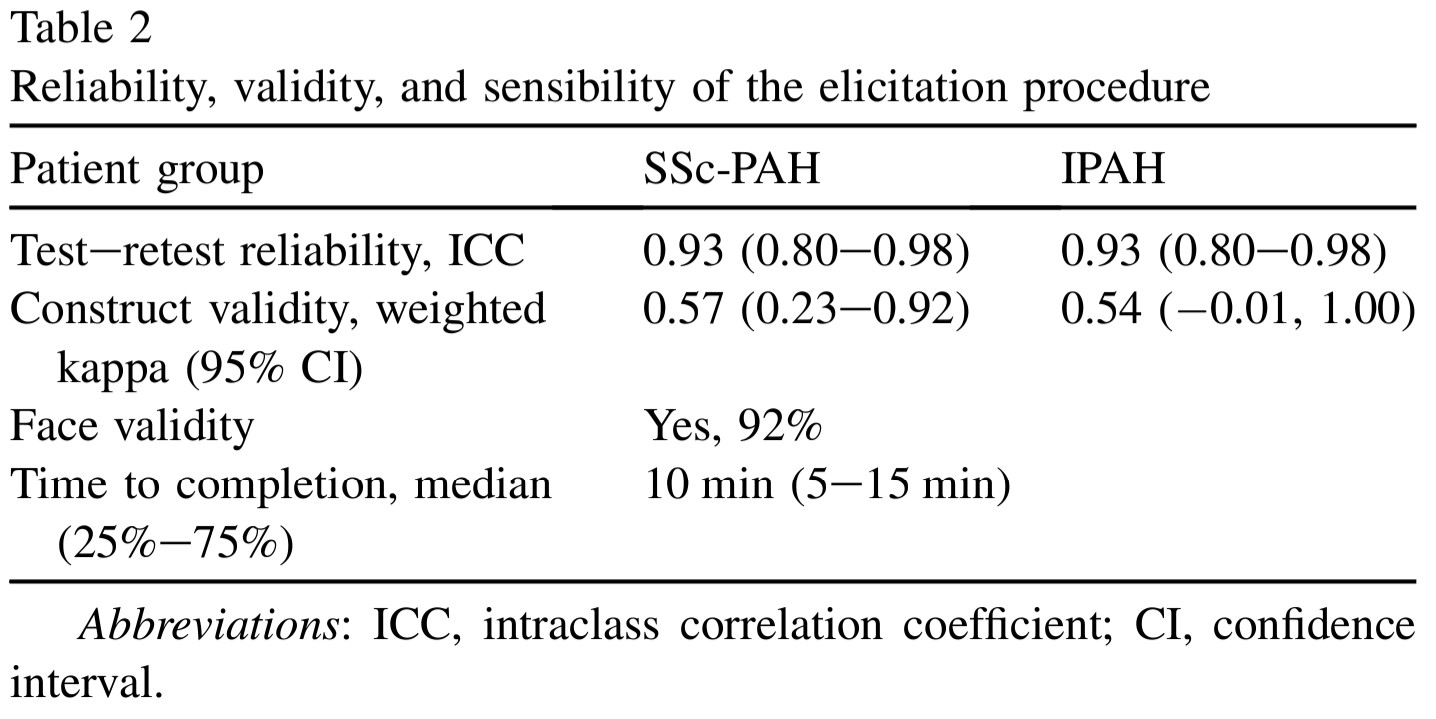
- Good validity, reliability, and feasibility
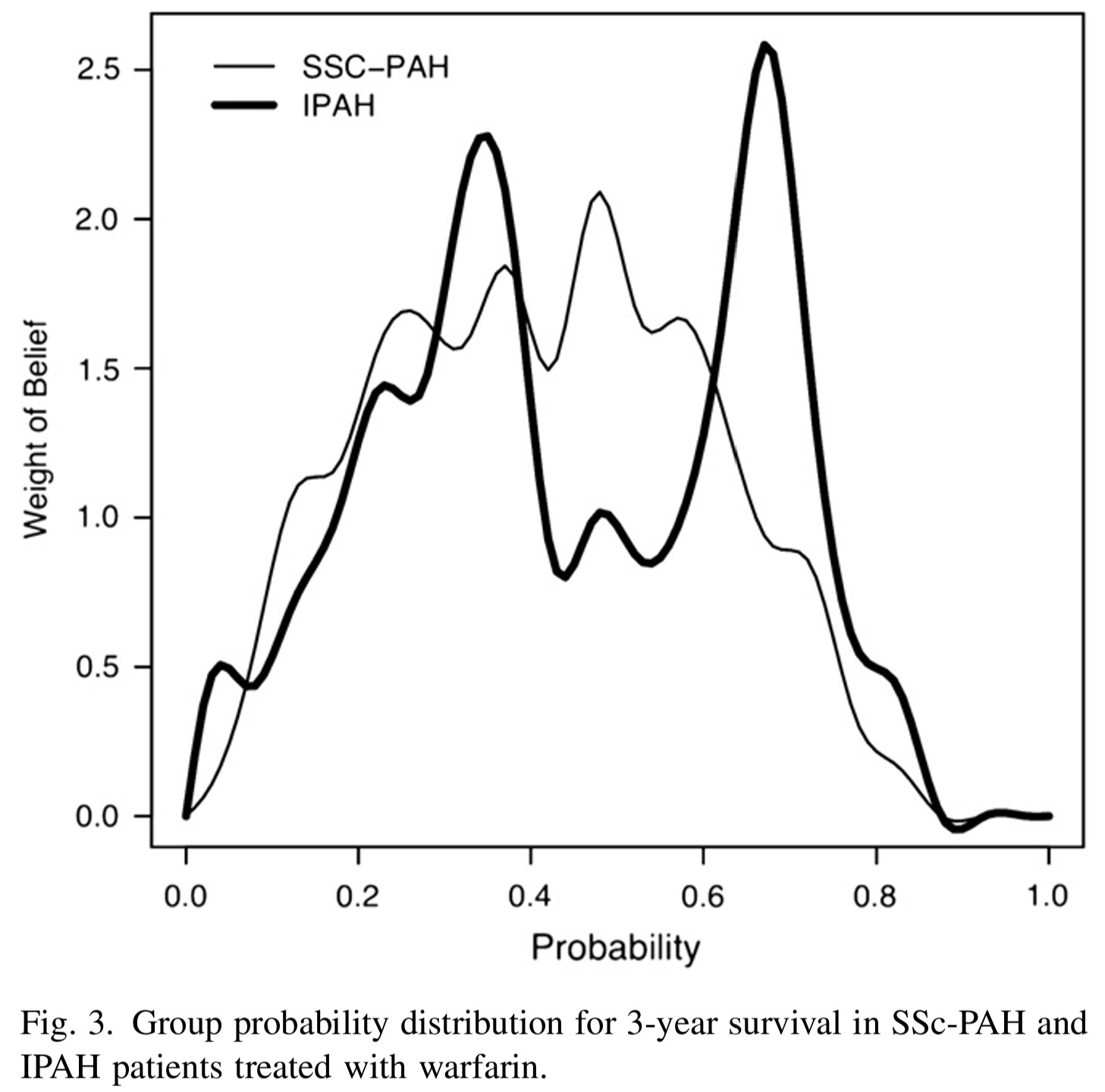
- The group probability distributions for SScPAH and IPAH patients treated with warfarin are wide.
- indicating variability in belief among experts
- The group probability distribution for SSc-PAH is unimodal and the group probability distribution for IPAH is bimodal.
- we can approximate these distributions using mixture distributions (see tutorial).
1.3 Default clincial priors
Section 5.5 Default Priors of (Spiegelhalter, Abrams, and Myles 2003)
“Non-informative” or “reference” priors
- It is attractive to use as a baseline analysis
- “making probability statements about parameters without being explicitly Bayesian”
- However, nonninformative priors are nonsensical and can lead to inference problems, especially in smaller samples
- can have a strong impact particularly when events are rare.
1. Non-informative Prior on Proportion
Suppose you are estimating the 30-day mortality after elective non-cardiac surgery, what is an uninformative prior for the proportion dying?
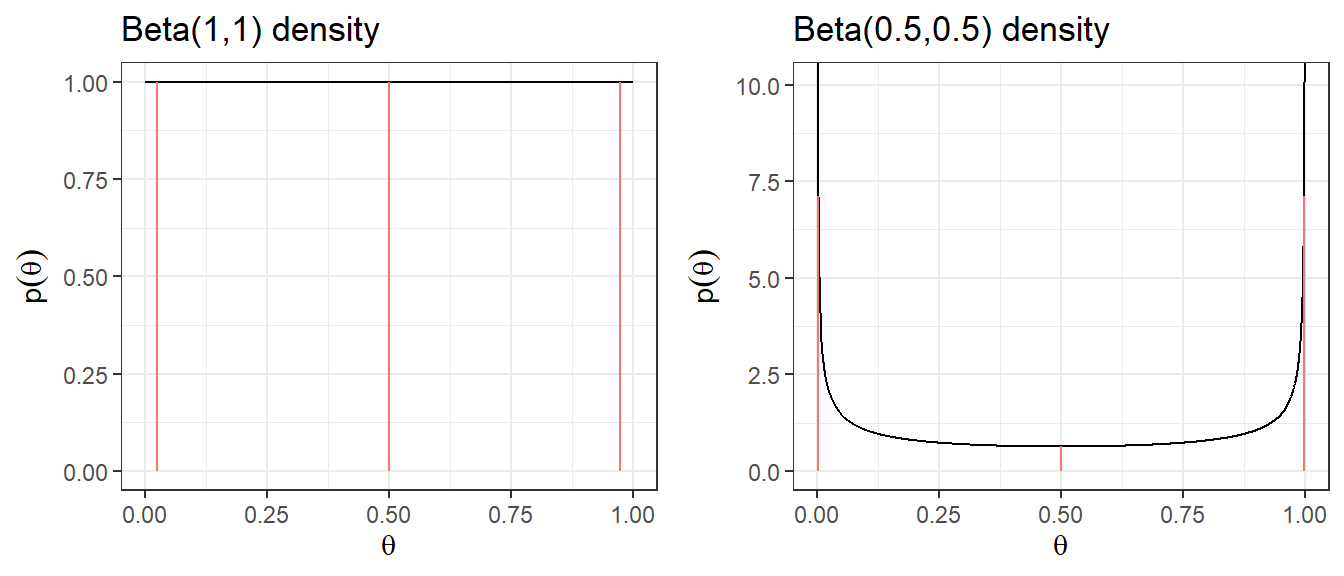
- An “off the shelf” uninformative priors for binomial model are
- \(\theta \sim U(0,1) \equiv Beta(1,1)\)
- Jeffreys prior, \(\theta \sim Beta(0.5,0.5)\), posterior estimates resemble frequentist estiamtes.
| Prior | median | q2.5 | q97.5 | Pr(\(\theta\)< 0.25) | Pr(\(\theta\)< 0.5) | Pr(\(\theta\)< 0.75) |
|---|---|---|---|---|---|---|
| Beta(1,1) | 0.5 | 0.025 | 0.975 | 0.25 | 0.5 | 0.75 |
| Beta(0.5,0.5) | 0.5 | 0.002 | 0.998 | 0.333 | 0.5 | 0.667 |
2. Non-informative Prior on log-relative risk
Suppose you want to estimate the relative risk for death in a clinical trial
Relative risk modelling works with the log-relative risk (as it has an approximately normal likelihood)
An “off the shelf” uninformative prior with a large variance might be \[\log(RR) = \theta \sim N(0, \sigma^2 = 10^2)\]
Prior 95% Credible Interval for log(RR) is -19.6 to 19.6
Prior 95% Credible Interval for RR is \(3 \times 10^{-9}\) to \(3 \times 10^{9}\)
A more sensible choice, \(N(0,5^2)\), for log scale OR, RR, and HR.
Code
plot.norm <- function(mu, sd){
d <- tibble(mu.plot=seq(-25,25, by=0.01),
density=dnorm(mu.plot, mu,sd))
p <- ggplot(data=d, aes(mu.plot, density))+
geom_line(col="black")+
geom_segment(aes(x = qnorm(0.025,mu,sd),
y = 0,
xend = qnorm(0.025,mu,sd),
yend = dnorm(qnorm(0.025,mu,sd), mu,sd),colour = "segment"))+
geom_segment(aes(x = qnorm(0.5,mu,sd),
y = 0,
xend = qnorm(0.5,mu,sd),
yend = dnorm(qnorm(0.5,mu,sd), mu,sd),colour = "segment"))+
geom_segment(aes(x = qnorm(0.975,mu,sd),
y = 0,
xend = qnorm(0.975,mu,sd),
yend = dnorm(qnorm(0.975,mu,sd), mu,sd),colour = "segment"))+
xlab(expression(mu))+
ylab(expression(p(mu)))+
ggtitle(paste0("N(",mu,",",sd^2,") density"))+
expand_limits(y=c(0,0.15))+
theme_bw()
p
}
ggarrange(plot.norm(0,10),
plot.norm(0,5),
plot.norm(0,4),
plot.norm(0,3),
nrow = 2,ncol=2, legend = "none")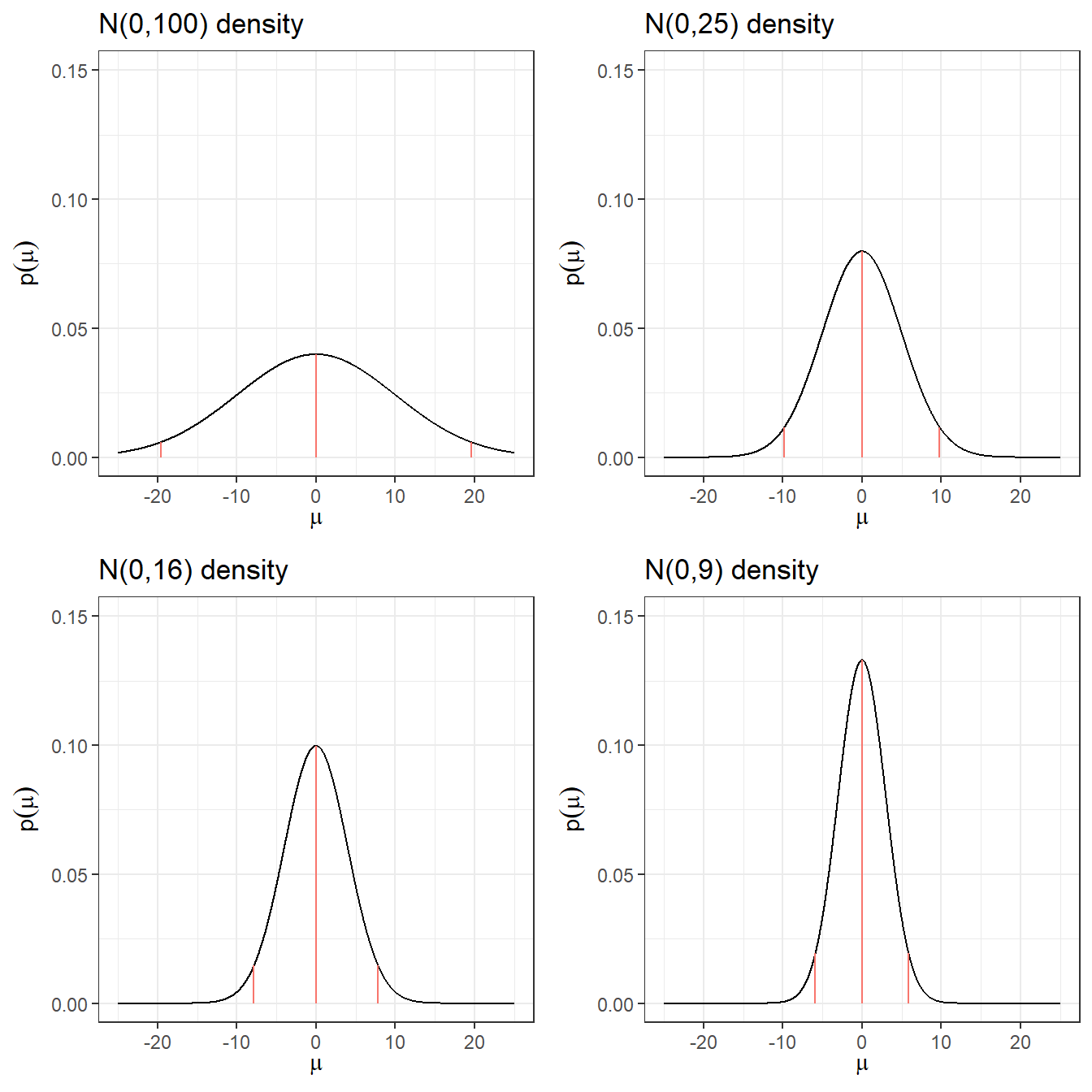
Code
res <- c("N(0,100)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 10),3),
round(exp(qnorm(0.025, 0, 10)),10),
round(exp(qnorm(0.975, 0, 10)),2))
res <- rbind(res, c("N(0,25)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 5),3),
round(exp(qnorm(0.025, 0, 5)),10),
round(exp(qnorm(0.975, 0, 5)),2))
)
res <- rbind(res, c("N(0,16)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 4),3),
round(exp(qnorm(0.025, 0, 4)),10),
round(exp(qnorm(0.975, 0, 4)),2))
)
res <- rbind(res, c("N(0,9)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 3),3),
round(exp(qnorm(0.025, 0, 3)),10),
round(exp(qnorm(0.975, 0, 3)),2))
)
res <- rbind(res, c("N(0,4)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 2),3),
round(exp(qnorm(0.025, 0, 2)),10),
round(exp(qnorm(0.975, 0, 2)),2))
)
res <- rbind(res, c("N(0,1)",
round(qnorm(c(0.5, 0.025, 0.975), 0, 1),3),
round(exp(qnorm(0.025, 0, 1)),10),
round(exp(qnorm(0.975, 0, 1)),2))
)
knitr::kable(res, row.names = F,
col.names = c("Prior log(RR)","median log(RR)","q2.5 log(RR)","q97.5 log(RR)","q2.5 RR","q97. RR"))| Prior log(RR) | median log(RR) | q2.5 log(RR) | q97.5 log(RR) | q2.5 RR | q97. RR |
|---|---|---|---|---|---|
| N(0,100) | 0 | -19.6 | 19.6 | 0.0000000031 | 325098849.19 |
| N(0,25) | 0 | -9.8 | 9.8 | 0.0000554616 | 18030.5 |
| N(0,16) | 0 | -7.84 | 7.84 | 0.0003937258 | 2539.84 |
| N(0,9) | 0 | -5.88 | 5.88 | 0.0027950873 | 357.77 |
| N(0,4) | 0 | -3.92 | 3.92 | 0.019842524 | 50.4 |
| N(0,1) | 0 | -1.96 | 1.96 | 0.1408634941 | 7.1 |
Quick Summary
- Posterior could land on implausible values with small numbers of deaths in one group or other.
- These issues resolve somewhat with larger data sets
- With a precise likelihood (e.g., large sample size or large number of events), data rescues you from allowing implausible values.
ISSUE with Uniform Priors
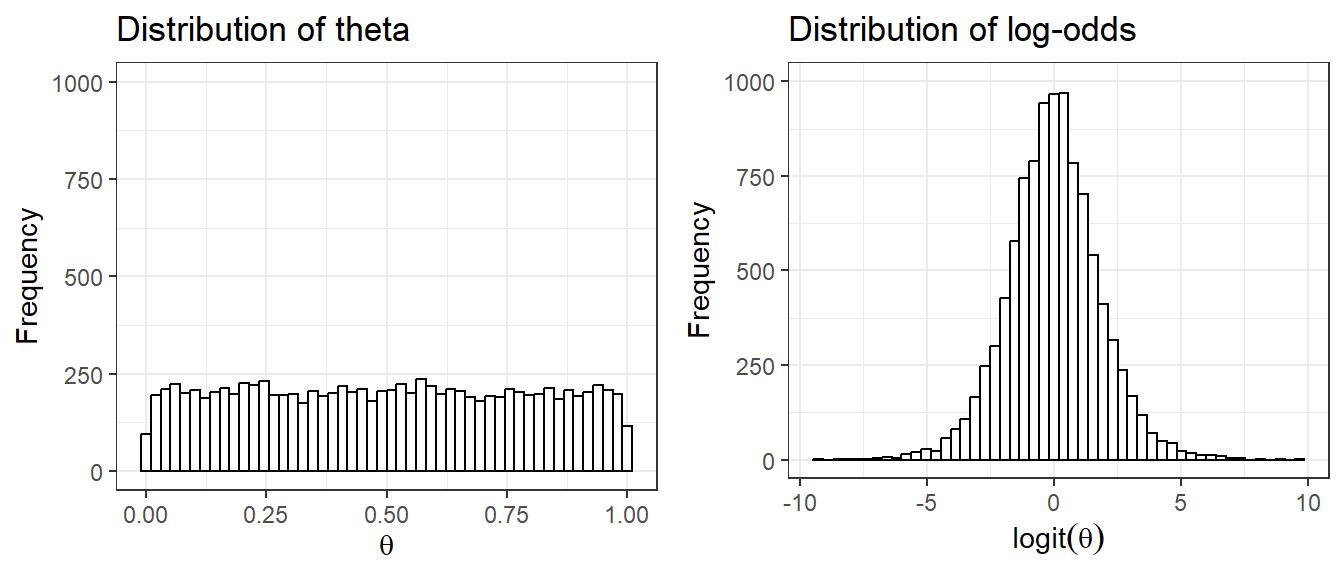
1. uniform priors on one scale are not uniform on a transformed scale
Suppose we set prior \(\theta \sim U(0,1)\) as an uninformative prior on the parameter quantifying risk of adverse event, probability \(\theta\)
- Prior distribution on log(\(\frac{\theta}{1-\theta}\)), which is also called the logit of \(\theta\) is no longer uniformly distributed
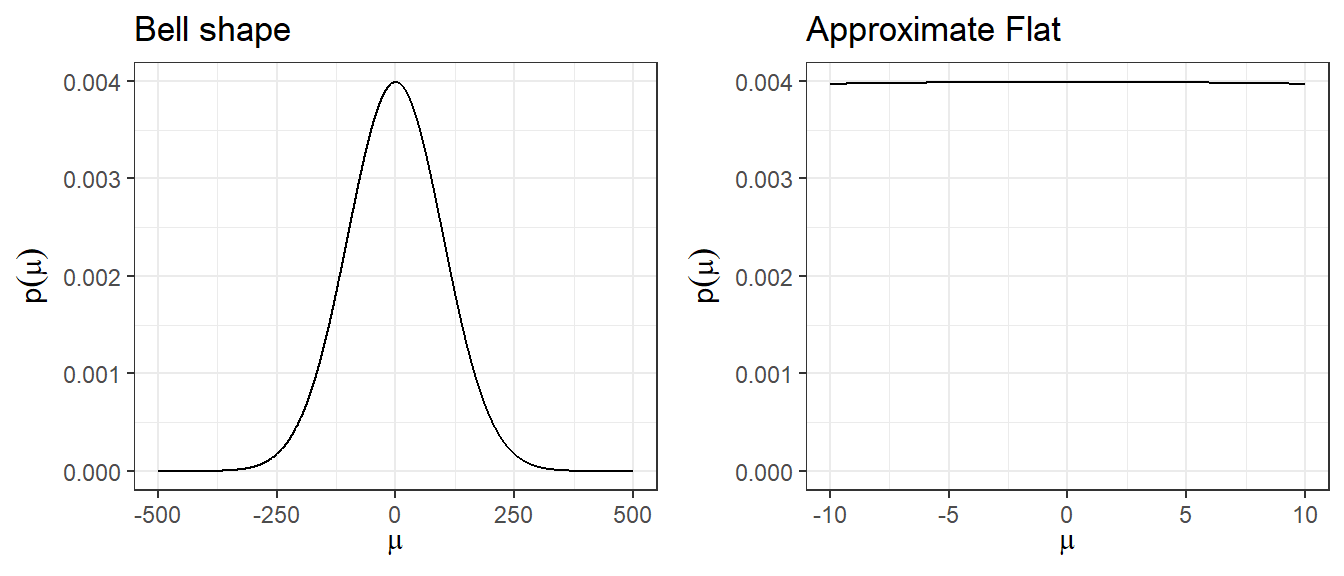
2. Using large variance normal distribution as non-informative prior
- How is a normal distribution N(0,\(100^2\)), with its bell-shape, uninformative?
- It does not put equal density on all points, as the density drops off from zero in each direction
- The key is that it is locally uniform
- In the region where a parameter is likely to lie, the normal distribution is flat.
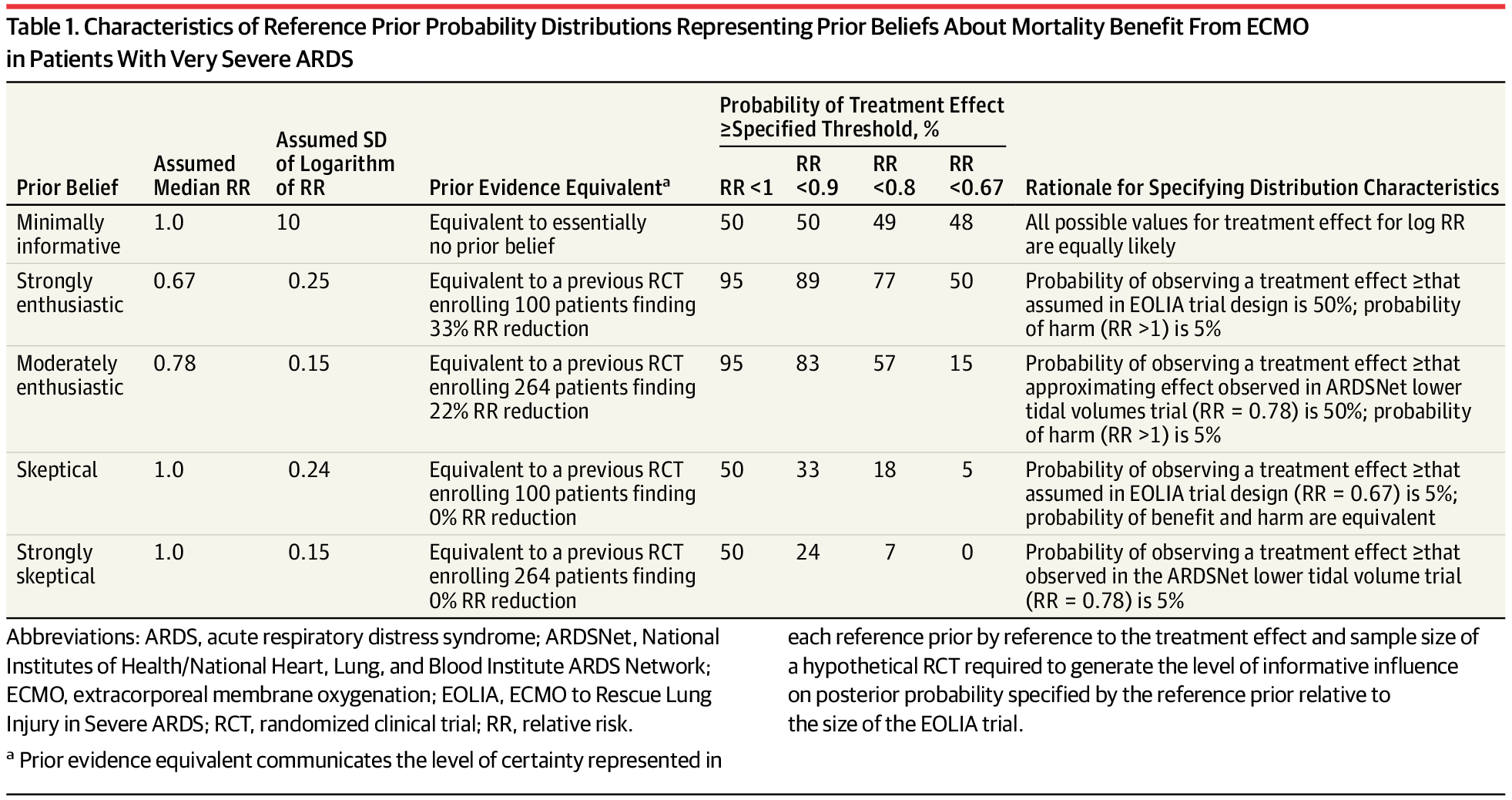
Minimally informative prior
- Use substantive knowledge to put most prior weight on possible values, without being too restrictive
From example, a RR for mortality in a trial, a prior with most weight on values of 0.66 to 1.5, a N(0,1) prior would be considered suitable.
For the between-person standard deviation of a 0-40 quality of life instrument, a prior with most weight on values under 10, a possible prior would be Gamma(0.1,0.1) on the precision.
Skeptical Prior
- priors that express doubts about large effects
- Mathematically speaking, a sceptical prior about a treatment effect will have a mean of zero and a shape chosen to include plausible treatment differences which determines the degree of scepticism.
- This is centred at no effect and a 95% CR extends to a minimally clinically important difference (MCID)
- Skeptical prior will “shrink” back observed results towards the null effect
- If under the skeptical prior, the posterior results support conclusion of effectiveness (results suggest departure from null), the skeptic is convinced!
- reasonable degree of scepticism maybe feeling that the study has been designed around an alternative hypothesis that is optimistic,
- formalized by a prior with only a small probability say 5% that the effect is as large as the optimistic alternative
Skeptical prior specification example from the EOLIA trial
- For the reanalysis of the EOLIA trial, the skeptical prior is defined as log(RR) ~ \(N(log(1), 0.24^2)\).
- MCID for 60-day mortality in RR comparing between ECMO and Rescue Lung Injury in Severe ARDS is 0.67, log(0.4/0.6) = -0.405.
- 0 (null, RR=1) will be the mean of the skeptical prior!
- Let P(RR<0.67) = P(log(RR)< -0.405) = 0.05, that is saying the probability of the ECOMO being effective beyond MCID is only 5%.
- Employee z transformation on normal distribution, we have
\[ P(log(RR)< -0.405) = P(\frac{log(RR)-0}{\sigma} < \frac{(-0.405) - 0}{\sigma}) = P(z < \frac{-0.405}{\sigma}) =0.05\]
\[ qnorm(0.05,0,1) \times \sigma = -0.405 \] \[\sigma = \frac{0.405}{qnorm(0.05,0,1)} = 0.246\]
- yielding a candidate skeptical prior on log(RR) ~ \(N(0,0.246^2)\)
Optimistic/enthusiastic prior
- This is centred at the MCID and a 95% CR extends to no effect
- Optimistic Prior will move observed results towards the MCID
- If a optimist is convinced that there is no effect, the evidence for no effect is strong
- For the reanalysis of the EOLIA trial, the strongly enthusiastic prior is defined as log(RR) ~ \(N(log(0.67), 0.25^2)\).
- An “enthusiastic” prior centred on the althernative hypothesis (meeting MCID) and with a low chance (say 5% probability) that the true treatment benefit is negative!
Strongly enthusiastic prior specification example from the EOLIA trial
- MCID for 60-day mortality in RR comparing between ECOMO and Rescue Lung Injury in Severe ARDS is 0.67, log(0.4/0.6) = -0.405.
- -0.405 will be the mean of the enthusiastic prior!
- Let P(RR>1) = P(log(RR)> 0) = 0.05, that is saying the probability of the ECMO not being effective is 5%.
- Employee z transformation on normal distribution, we have
\[ P(log(RR)> 0) = P(\frac{log(RR)-(-0.405)}{\sigma}> \frac{0-(-0.405)}{\sigma}) = P(z > \frac{0.405}{\sigma}) =0.05\] \[P(z < \frac{0.405}{\sigma}) = 1- 0.05 = 0.95\] \[qnorm(0.95,0,1) \times \sigma = 0.405\] \[\sigma = \frac{0.405}{qnorm(0.95,0,1)} = 0.246\]
- yielding a candidate enthusiastic prior on log(RR) ~ \(N(log(0.67),0.246^2)\)
1.4 Historical data
- Incorporating historical data in Bayesian analysis
- these can be formalized as a means of using past evidence as a basis for a prior distribution for a parameter of interest
- Meta-analysis is a very useful tool for evidence synthesis in clinical research
- We can directly use published meta-analysis results to construct priors
- if not available, one can also complete a meta-analysis to synthesis evidence for prior construction
- These types of prior are called data-derived priors.
- For example, in the Bayesian reanalysis of the EOLIA trial, data-derived priors are constructed from a Bayesian meta-analysis of published relevant studies.
- The posterior distribution (updated belief) of treatment effect is produced by combining data-derived prior with data from the current study.
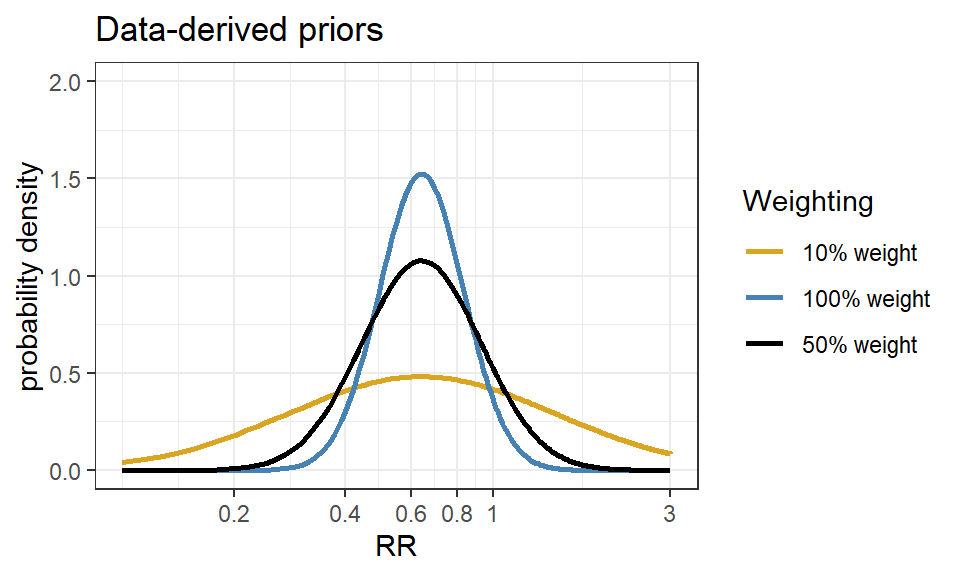
Downweighting:
To reflect concerns about possible differences between the current and previous studies, the variance of the past studies can be inflated to receive less weight in the analysis on the pooled estimate of effect.
Data-derived prior from the Bayesian reanalysis of the EOLIA trial(Goligher et al. 2018)
- Data-derived prior was developed based on three relevant studies from a meta-analysis of ECMO for ARDS (Munshi et al. 2014)
- Three studies are (Peek et al. 2009), (Pham et al. 2013), and (Noah et al. 2011)
- After fitting a random effect model, the pooled RR is estimated as 0.64 with 95% CI (0.38 - 1.06).
- We now express this prior as a normal likelihood on the log(RR) scale and consider three scenarios of “downweighting” (10%, 50% and 100%).
Code
dmeta <- tibble(
study = c("Peek 2009", "Noah 2011", "Pham 2013"),
event.e = c(25,18,35),
n.e = c(68,75,98),
event.c = c(44,38,54),
n.c = c(90,75,98)
)
library(meta)
m.bin <- metabin(event.e = event.e,
n.e = n.e,
event.c = event.c,
n.c = n.c,
studlab = study,
data = dmeta,
sm = "RR",
method = "MH",
MH.exact = TRUE,
fixed = FALSE,
random = TRUE,
method.tau = "REML",
hakn = TRUE,
title = "Mortality")
summary(m.bin)Review: Mortality
RR 95%-CI %W(random)
Peek 2009 0.7520 [0.5160; 1.0959] 32.8
Noah 2011 0.4737 [0.2989; 0.7507] 21.9
Pham 2013 0.6481 [0.4706; 0.8927] 45.3
Number of studies: k = 3
Number of observations: o = 504 (o.e = 241, o.c = 263)
Number of events: e = 214
RR 95%-CI t p-value
Random effects model 0.6353 [0.3805; 1.0607] -3.81 0.0626
Quantifying heterogeneity (with 95%-CIs):
tau^2 < 0.0001 [0.0000; 2.1514]; tau = 0.0013 [0.0000; 1.4668]
I^2 = 14.8% [0.0%; 91.1%]; H = 1.08 [1.00; 3.36]
Test of heterogeneity:
Q d.f. p-value
2.35 2 0.3093
Details of meta-analysis methods:
- Inverse variance method
- Restricted maximum-likelihood estimator for tau^2
- Q-Profile method for confidence interval of tau^2 and tau
- Calculation of I^2 based on Q
- Hartung-Knapp adjustment for random effects model (df = 2)Code
CI.normal <- log(c(0.38, 1.06))
sigma <- (CI.normal[2] - CI.normal[1])/(2*1.96)
mu <- log(0.64)
xlabs <- c(0.2, 0.4, 0.6, 0.8, 1, 3)
noweight <- dnorm(log(seq(0.1,3, length=201)), mu, sigma)
weight50 <- dnorm(log(seq(0.1,3, length=201)), mu, sigma/sqrt(0.5))
weight10 <- dnorm(log(seq(0.1,3, length=201)), mu, sigma/sqrt(0.1))
d <- data.frame(logrr.range = rep(log(seq(0.1,3, length=201)),3),
plog.rr = c(noweight, weight50, weight10),
Weighting = rep(c("100% weight","50% weight","10% weight"),each=201))
ggplot(d, aes(logrr.range, plog.rr,colour=Weighting))+
geom_line(size = 1)+
xlab("RR")+
ylab("probability density")+
ylim(c(0,2))+
scale_x_continuous(breaks = log(xlabs),labels=xlabs, limits=c(log(0.1), log(3)))+
scale_colour_manual(values=c("goldenrod","steelblue","black"))+
theme_bw()+
ggtitle("Data-derived priors")
References
Goligher, Ewan C, George Tomlinson, David Hajage, Duminda N Wijeysundera, Eddy Fan, Peter Jüni, Daniel Brodie, Arthur S Slutsky, and Alain Combes. 2018. “Extracorporeal Membrane Oxygenation for Severe Acute Respiratory Distress Syndrome and Posterior Probability of Mortality Benefit in a Post Hoc Bayesian Analysis of a Randomized Clinical Trial.” Jama 320 (21): 2251–59.
Johnson, Sindhu R, George A Tomlinson, Gillian A Hawker, John T Granton, and Brian M Feldman. 2010. “Methods to Elicit Beliefs for Bayesian Priors: A Systematic Review.” Journal of Clinical Epidemiology 63 (4): 355–69.
Johnson, Sindhu R, George A Tomlinson, Gillian A Hawker, John T Granton, Haddas A Grosbein, and Brian M Feldman. 2010. “A Valid and Reliable Belief Elicitation Method for Bayesian Priors.” Journal of Clinical Epidemiology 63 (4): 370–83.
Lesaffre, Emmanuel, Gianluca Baio, and Bruno Boulanger. 2020. Bayesian Methods in Pharmaceutical Research. CRC Press.
Munshi, Laveena, Teagan Telesnicki, Allan Walkey, and Eddy Fan. 2014. “Extracorporeal Life Support for Acute Respiratory Failure. A Systematic Review and Metaanalysis.” Annals of the American Thoracic Society 11 (5): 802–10.
Noah, Moronke A, Giles J Peek, Simon J Finney, Mark J Griffiths, David A Harrison, Richard Grieve, M Zia Sadique, et al. 2011. “Referral to an Extracorporeal Membrane Oxygenation Center and Mortality Among Patients with Severe 2009 Influenza a (H1N1).” Jama 306 (15): 1659–68.
O’Hagan, Anthony, Caitlin E Buck, Alireza Daneshkhah, J Richard Eiser, Paul H Garthwaite, David J Jenkinson, Jeremy E Oakley, and Tim Rakow. 2006. “Uncertain Judgements: Eliciting Experts’ Probabilities.”
Peek, Giles J, Miranda Mugford, Ravindranath Tiruvoipati, Andrew Wilson, Elizabeth Allen, Mariamma M Thalanany, Clare L Hibbert, et al. 2009. “Efficacy and Economic Assessment of Conventional Ventilatory Support Versus Extracorporeal Membrane Oxygenation for Severe Adult Respiratory Failure (CESAR): A Multicentre Randomised Controlled Trial.” The Lancet 374 (9698): 1351–63.
Pham, Tài, Alain Combes, Hadrien Rozé, Sylvie Chevret, Alain Mercat, Antoine Roch, Bruno Mourvillier, et al. 2013. “Extracorporeal Membrane Oxygenation for Pandemic Influenza a (H1N1)–Induced Acute Respiratory Distress Syndrome: A Cohort Study and Propensity-Matched Analysis.” American Journal of Respiratory and Critical Care Medicine 187 (3): 276–85.
Spiegelhalter, David J., Keith R. Abrams, and Jonathan P. Myles. 2003. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. John Wiley & Sons, Ltd. https://doi.org/10.1002/0470092602.