require(tidyverse)
library(extraDistr)Tutorial 3
Hands-on exercise on prior elicitation
1. The BIPED Study
Project: Remote expert elicitation to determine the prior probability distribution for Bayesian sample size determination in international randomized controlled trials: Bronchiolitis in Infants Placebo Versus Epinephrine and Dexamethasone (BIPED) Study
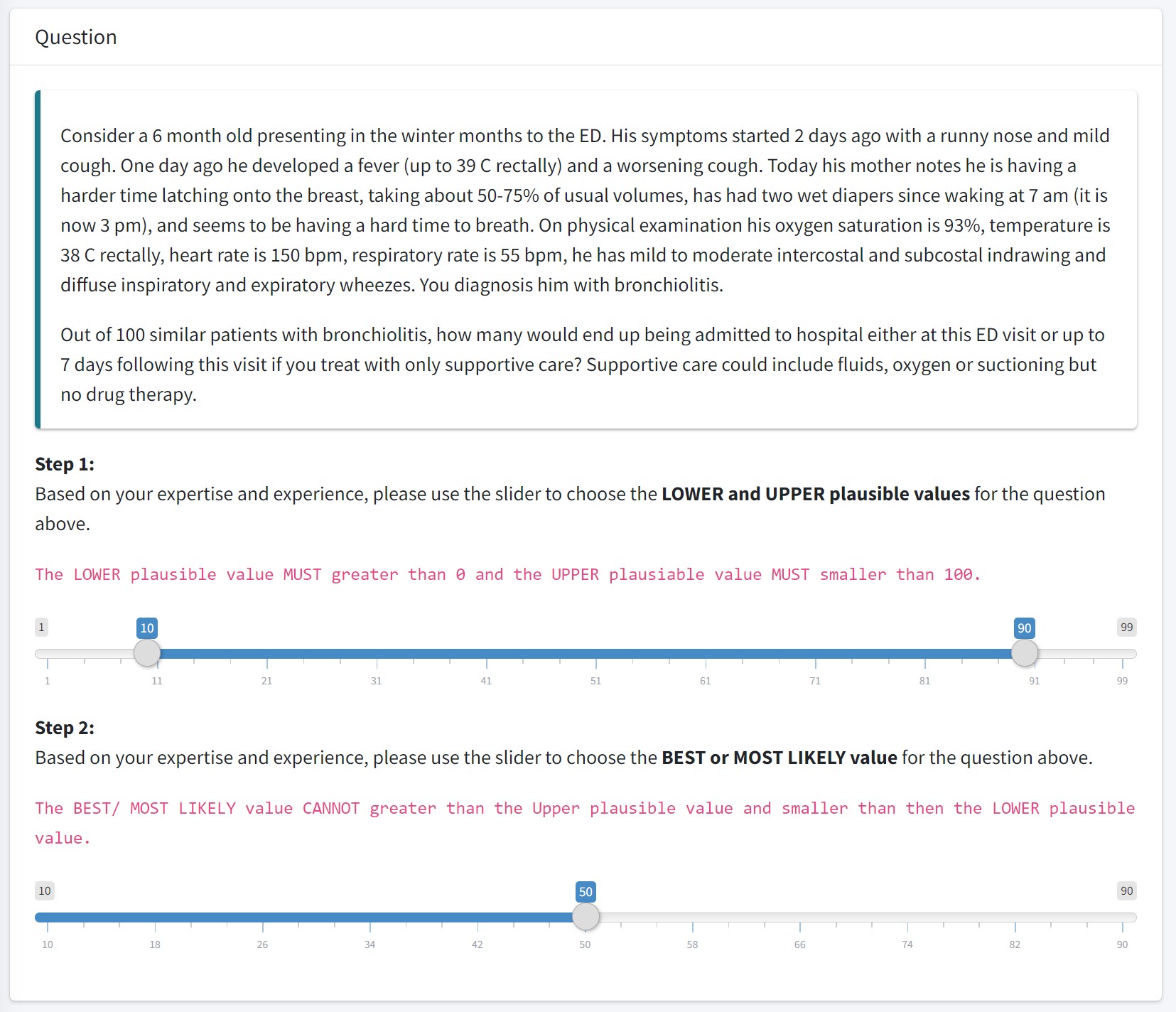
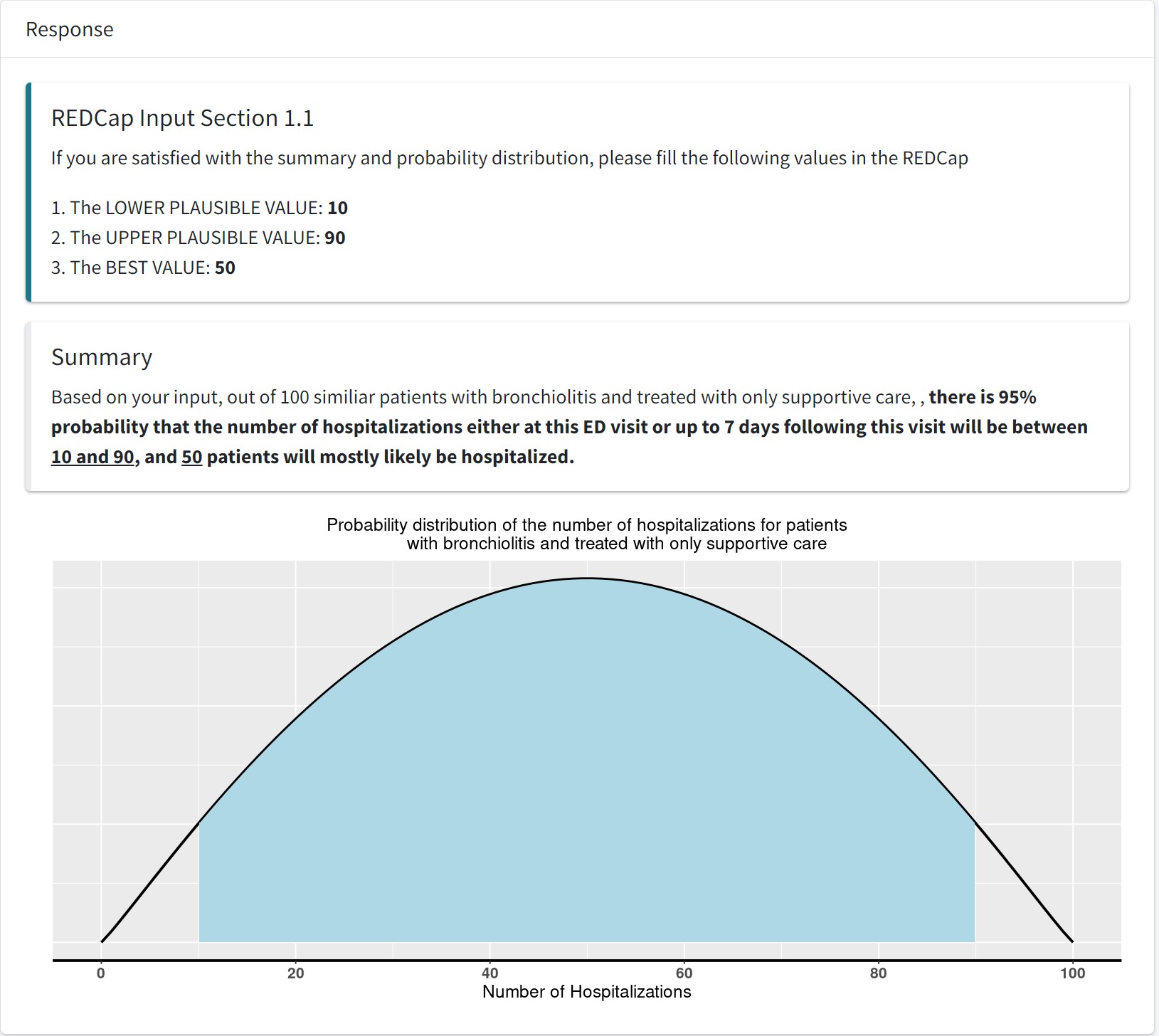
1.1 Given a range of beliefed pausible value, how can we calculate beta distribution parameters?
- Mathematically, we are solving for \(\alpha\) and \(\beta\) given L and U and the mode (“best value”);
\[P(L < \theta < U) = 0.95\] \[\theta \sim Beta(\alpha, \beta)\] - Let \(\theta\) be the number of patient end up being admitted to hospital out of 100 similar patients with bronchiolitis
- Suppose expert A pick the range as [10,90], that is \(P(10<\theta<90)=0.95\) and if we assume \(\theta\) follows a Beta distribution, and the mode, \(50 = \frac{\alpha-1}{\alpha+\beta-2}\) can we find the corresponding \(\alpha\) and \(\beta\) of this beta distribution?
- Given 95% CR, how to reverse calculation to get Beta distribution parameters: alpha and beta;
- We can use maximum likelihood estimation (MLE)! A statistical estimation method that helps us to identify a parametric distribution using empirical percentile.
# For this calculation we want to use beta-binomial distribution;
# This is because the confidence region in the BIPED app is reported on the number of events out of 100 standard patients.
# let's write out the likelihood of beta-binomial model
expert_beta <- function(L, U, mode, level = 0.95) {
stopifnot(0 < L, L < U, U < 1,
0 < mode, mode < 1,
level > 0, level < 1)
# One-dimensional objective: log-k keeps the search on (0,???)
objective <- function(logk) {
k <- exp(logk)
alpha <- 1 + mode * k
beta <- 1 + (1 - mode) * k
q_low <- qbeta( (1 - level)/2, alpha, beta )
q_high <- qbeta( 1 - (1 - level)/2, alpha, beta )
(q_low - L)^2 + (q_high - U)^2
}
opt <- optimize(objective, interval = c(-15, 25)) # log-scale search
k <- exp(opt$minimum)
list(alpha = 1 + mode * k,
beta = 1 + (1 - mode) * k,
SSE = opt$objective) # residual mis-fit (???0 if feasible)
}
# Maximize the likelihood using optim function;
expert_beta(L = 10/100, U = 90/100, mode = 50/100)$alpha
[1] 2.093438
$beta
[1] 2.093438
$SSE
[1] 4.746533e-15- Expert A selected a \(Beta(\alpha = 2.093438, \beta = 2.093438)\)
# we can create a R function to efficiently generate plots;
beta_plot <- function(shape1=1, shape2=1, scale = 100){
# creating x vector;
x <- seq(from = 0, to = 1, by = 0.001)
# finding density probability for each x element;
y <- dbeta(x, shape1 = shape1, shape2 = shape2)
# create a plotting dataframe;
data <- data.frame(x,y)
# ggplot;
ggplot(data, aes(x=x*scale, y=y)) +
geom_line() +
labs(x=bquote(.(scale) * theta), y='density', title=paste0('Beta(',shape1,',',shape2,')'))+
theme_bw()
}
beta_plot(2.093438,2.093438)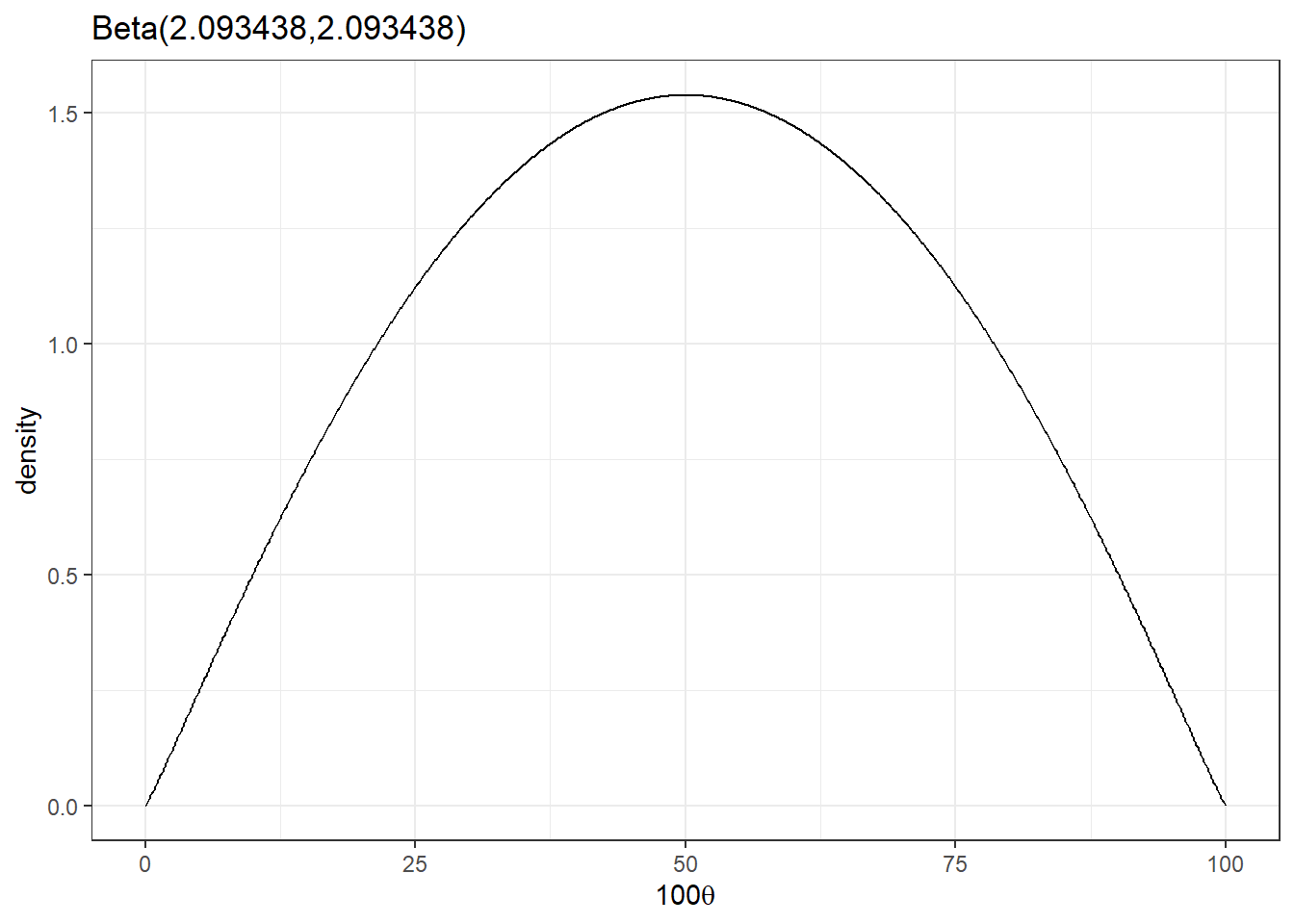
- What is the expected number of hospitalization? (mean of the beta distribution)
\[100 \times \frac{2.093438}{2.093438+2.093438} = 50 \]
- Suppose expert B pick the range as [50,90] and mode 80, what is expert B’s Beta distribution?
beta_parameters<-expert_beta(L = 50/100, U = 90/100, mode = 80/100)
beta_plot(beta_parameters$alpha,beta_parameters$beta)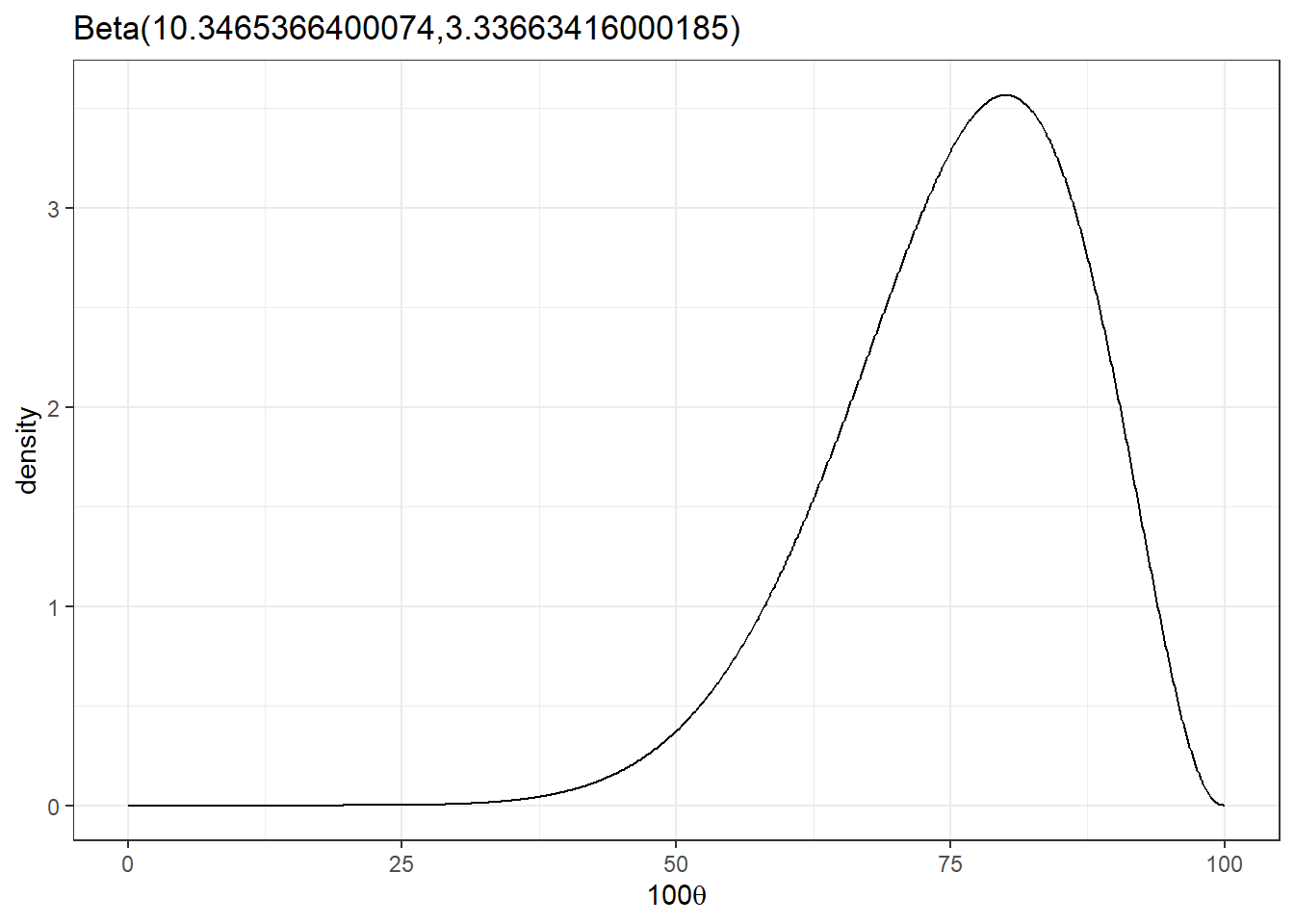
mean = 100*(beta_parameters$alpha/(beta_parameters$alpha+beta_parameters$beta))
mean[1] 75.615051.2 Combine multiple expert options - (pooled) mixture distribution
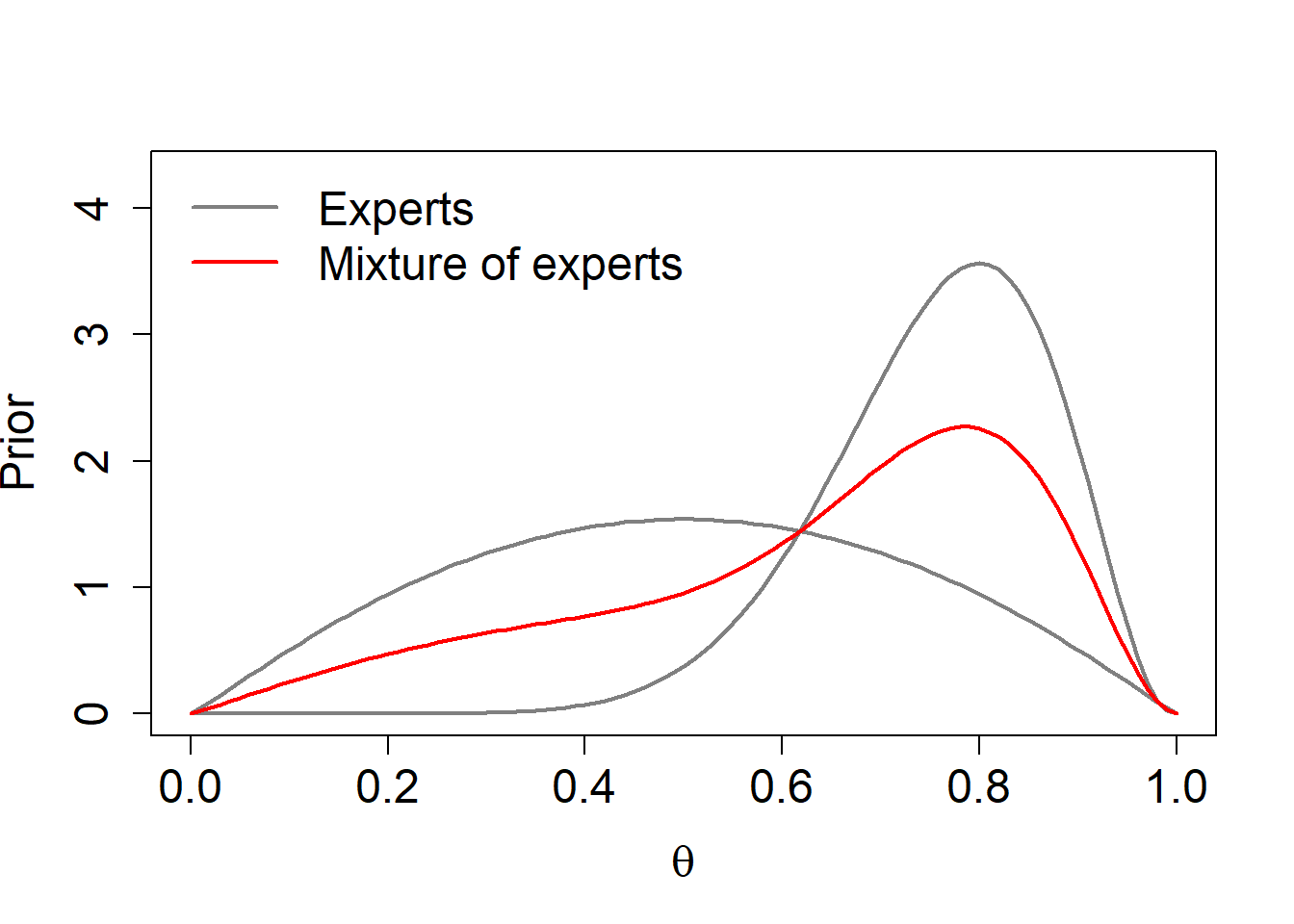
a1 <- 2.09
b1 <- 2.09
a2 <- 10.35
b2 <- 3.34
w <- c(1/2,1/2) #assign equal mixture weight to the two believes;
theta <- seq(0,1,0.01)
p1 <- dbeta(theta,a1,b1)
p2 <- dbeta(theta,a2,b2)
pool <- w[1]*p1+w[2]*p2
r <- 1.2*max(c(p1,p2, pool))
plot(theta,p1,col=gray(0.5),lwd=2,ylim=c(0,r),type="l",
xlab=expression(theta),ylab="Prior",
cex.lab=1.5,cex.axis=1.5)
lines(theta,p2,col=gray(0.5),lwd=2)
lines(theta,pool,col="red",lwd=2)
legend("topleft",c("Experts","Mixture of experts"),lwd=2,col=c(gray(0.5), "red"),bty="n",cex=1.5)